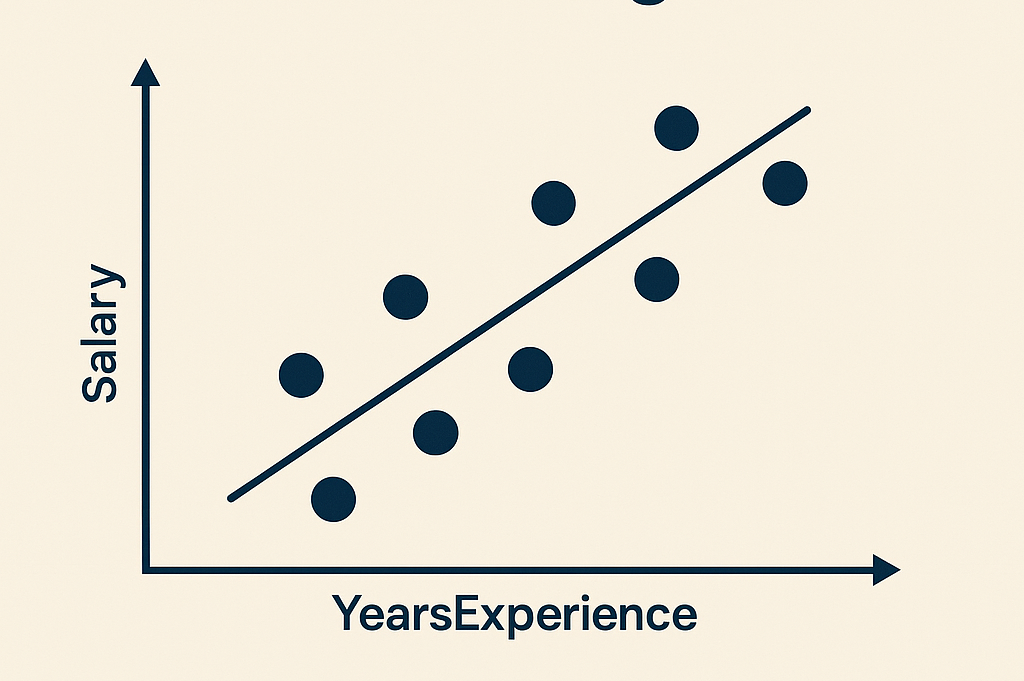
Salary Prediction with Linear Regression
Un projet de machine learning simple prédictant le salaire basé sur les années d'expérience en utilisant la régression linéaire univariée.
Vue d'ensemble du projet
Ce projet démontre l'implémentation de la régression linéaire à partir de zéro et avec scikit-learn. Le dataset contient les années d'expérience comme feature et le salaire comme cible. Le projet couvre l'exploration des données, la vérification des doublons et valeurs nulles, l'implémentation de la fonction de coût, l'optimisation par descente de gradient, et l'évaluation du modèle.
Les résultats sont visualisés avec des lignes de régression et comparés avec sklearn's LinearRegression.
Ce projet construit une base solide en machine learning en implémentant l'un des algorithmes fondamentaux (régression linéaire). Il améliore la compréhension mathématique, la pratique du codage avec NumPy, et l'expérience pratique avec l'entraînement, la visualisation et la validation de modèles.
Fonctionnalités clés
Implémentation du code
1. Import des bibliothèques
import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression
2. Chargement du dataset
# Chargement du dataset
df = pd.read_csv("Salary_Data.csv")
df.head()3. Fonction de coût (MSE)
def compute_cost(x, y, w, b):
m = len(x)
total_cost = 0
for i in range(m):
total_cost += (w * x.iloc[i, 0] + b - y.iloc[i, 0])**2
return total_cost / (2 * m)
# Test initial
w, b = 0, 0
print("Coût initial (w=0, b=0):", compute_cost(X, y, w, b))4. Algorithme de descente de gradient
def gradient_descent(x, y, w, b, alpha, num_iters):
m = len(x)
cost_history = []
for _ in range(num_iters):
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x.iloc[i, 0] + b # prédiction
err = f_wb - y.iloc[i, 0] # erreur
dj_dw += err * x.iloc[i, 0]
dj_db += err
dj_dw /= m
dj_db /= m
# mise à jour des paramètres
w = w - alpha * dj_dw
b = b - alpha * dj_db
# sauvegarde du coût pour le suivi
cost_history.append(compute_cost(x, y, w, b))
return w, b, cost_history
# Exécution de la descente de gradient
w_init, b_init = 0, 0
alpha = 0.01
num_iters = 1000
w_final, b_final, J_history = gradient_descent(X, y, w_init, b_init, alpha, num_iters)5. Visualisation des résultats
# Visualisation de la réduction du coût
plt.plot(J_history)
plt.xlabel("Itération")
plt.ylabel("Coût J")
plt.title("Réduction du coût à travers les itérations")
plt.show()
# Ligne de régression
plt.scatter(X, y, label="Données d'entraînement")
plt.plot(X, w_final * X + b_final, color="red", label="Ligne de régression")
plt.xlabel("Années d'expérience")
plt.ylabel("Salaire")
plt.title("Régression linéaire (implémentation manuelle)")
plt.legend()
plt.show()6. Comparaison avec scikit-learn
# Modèle scikit-learn
model = LinearRegression()
model.fit(X, y)
print("Coefficients scikit-learn:")
print("w =", model.coef_[0][0])
print("b =", model.intercept_[0])
# Visualisation comparative
plt.scatter(X, y, label="Données d'entraînement")
plt.plot(X, model.predict(X), color="green", label="Ligne de régression sklearn")
plt.xlabel("Années d'expérience")
plt.ylabel("Salaire")
plt.title("Régression linéaire (scikit-learn)")
plt.legend()
plt.show()Détails du projet
Client
Projet Personnel
Timeline
2025 – Présent
Rôle
Développeur Machine Learning
À propos du dataset
Autres projets

JobHub – Plateforme d'Emploi Intelligente avec Agent IA
Application Web Full-Stack

Email AI Platform
Intelligence Artificielle

Ovia
Intelligence Artificielle

MediBook Platform
Web Application (Healthcare SaaS)

MediBook Healthcare Passport
Web Application (Healthcare SaaS)

MediBook Pharma Platform
Web Application (Healthcare SaaS)

MediBook Laboratory Platform
Web Application (Healthcare SaaS)
Personal Portfolio Website
Web Application
Reboturn
E-Commerce Platform (Eco-Conscious SaaS)

Insurance Cost Prediction with Multivariable Linear Regression
Machine Learning Project
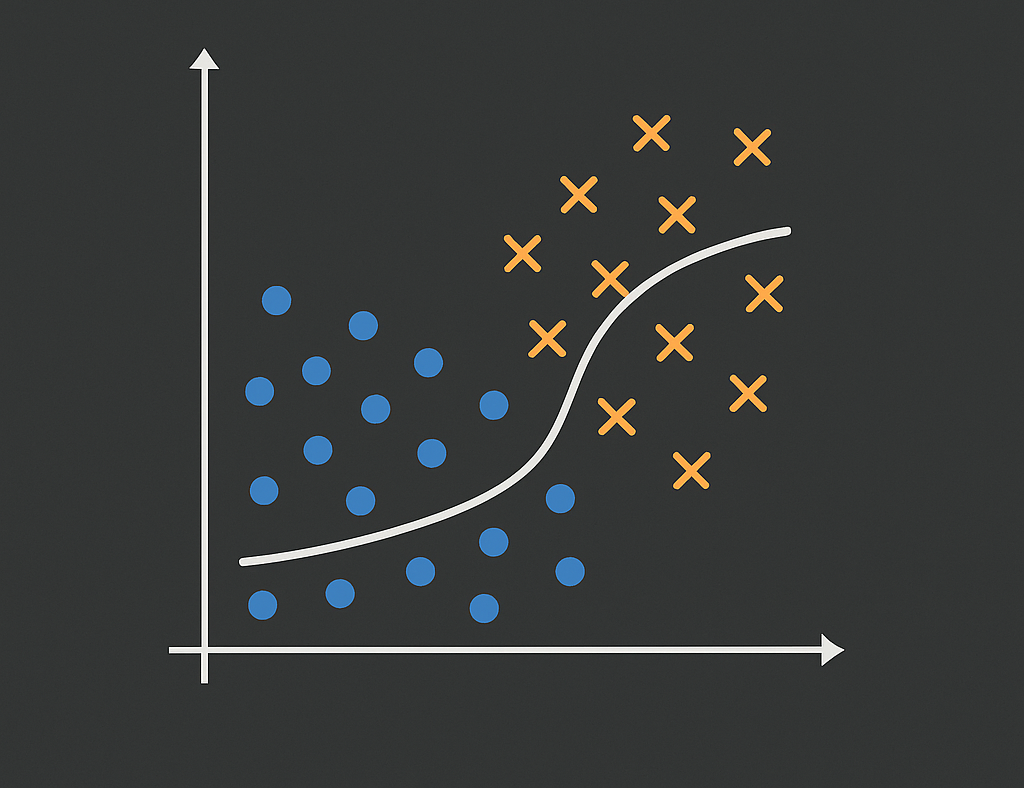
Logistic Regression (Classification)
Machine Learning Project

Brain Tumor Classification (Deep Learning - CNN)
Machine Learning Project

Decision Trees
Machine Learning Project

Random Forest
Machine Learning Project

Clustering (K-means)
Machine Learning Project

Anomaly Detection
Machine Learning Project

Système de Recommandation Netflix
Intelligence Artificielle

Recommender Systems (Content-based Filtering)
Machine Learning Project

VelociType — Test de Vitesse de Frappe
Application Python

Watermark — Application de Filigrane d'Images
Application Python

XO Battle — Jeu de Tic-Tac-Toe
Jeu Python
PulseCode — Morse Converter
Application Python
© 2025 Sina Ganji. Tous droits réservés.